“Three Millennia of Logic” (50 minutes)
“A Wonderful Company” (50 minutes)

In 1645, the French mathematician Blaise Pascal built the first true mechanical calculator, known as the Pascaline. The Pascaline was capable of performing relatively simple mathematical calculations. This small-sized machine consisted of pulleys that, when rotated by the user, displayed the results. The original “computer” had five gears, allowing calculations with relatively small numbers, but later versions were built with six and eight gears. This machine could perform only two operations: addition and subtraction.
At the top of the Pascaline, there was a row of toothed wheels, known as gears, each containing the numbers from 0 to 9. The first wheel represented units, the second tens, the third hundreds, and so on.
In 1673, the mathematician and philosopher Gottfried Wilhelm
Leibniz (1646-1716) improved Pascal’s machine by creating a manual calculating machine that could perform multiplication and division besides addition and subtraction. During the early stages of his career, Leibniz also invented the binary number system (0 and 1), which remains the foundation of modern computer programming languages. This machine is currently preserved in a technical museum in Germany.

The English mathematician, philosopher, and logician George Boole (1815–1864), through his two works:
- "The Mathematical Analysis of Logic" (1847)
- "An Investigation of the Laws of Thought on Which the Mathematical Theories of Logic and Probabilities" (1854)
transformed propositional logic into an algebraic system, known as Boolean Algebra, which operates on the set B = , equipped with the operations "+" (OR) and "•" (AND).
Boolean Logic and Aristotelian Logic
Aristotelian logic, which states that "it is impossible for the same property to belong and not belong to the same object" (principle of contradiction), is translated in Boolean Algebra as "nothing can simultaneously belong and not belong to a given class."
Boole's system was built upon the principles of classical algebra, but with a very specific structure. Unlike elementary algebra, where variables take numerical values and the main operations are addition and multiplication, Boolean Algebra uses only two values, "1" and "0". Additionally, it introduces three fundamental operations:
- Conjunction ("Λ") (AND)
- Disjunction ("V") (OR)
- Negation ("-") (NOT)
Boolean algebra forms the foundation of modern digital circuits and computer logic, making it essential in computer science and programming.

Friedrich Ludwig Gottlob Frege (1848–1925) and the Foundations of Modern Programming Languages
Friedrich Ludwig Gottlob Frege was a German mathematician, logician, and philosopher who laid the foundation for modern programming languages.
His work in logic, the philosophy of mathematics, philosophical logic, and the theory of meaning became the starting point and reference for subsequent research in these fields. Frege introduced a symbolic logic system that significantly extended Aristotelian logic and attempted to reduce arithmetic to logic, demonstrating that arithmetic propositions are analytic. He also introduced two central concepts in the theory of meaning: sense (“Sinn”) and reference (“Bedeutung”).
Frege’s Theory of Meaning
Frege’s research in the theory of meaning originated from his pursuit of a conceptual notation system for pure thought, which would allow for the most reliable verification of logical reasoning and reveal all hidden assumptions involved in arguments.
This symbolic system aimed to realize Leibniz’s ideal of a universal language, a formal system in which logical validity could be objectively determined. Within this framework, Frege distinguished between sense and reference, separating linguistic meaning from subjective mental representations and psychological events.
Frege’s theory of meaning is based on this distinction between sense and reference and was developed in response to:
- The rejection of a simplistic representational view of meaning, which assumes that meaning is merely a link between words and objects.
- The rejection of psychologism, the idea that meaning is a psychological entity and that logical relationships are merely psychological associations.
According to Frege, the meaning of a linguistic expression is not simply a direct association between the expression and an object, nor is it merely a mental image or representation. Instead, meaning is an abstract, logical structure that determines how expressions relate to one another within a formal system.
Impact on Computer Science and Logic
Frege’s contributions laid the groundwork for modern formal logic, which in turn influenced computer science, artificial intelligence, and programming language theory. His formalization of logic inspired the development of predicate logic, which serves as the foundation for automated reasoning, computational logic, and programming languages today.
“Two Numbers Are More Than Enough” (70 minutes)

The Transition to Technology – From Abstract to Tangible – Data Structures and Organization (Δομές δεδομένων)
In modern computer technology, the organization of data is fundamental to the efficient operation of systems. The transition from the abstract—the logical and mathematical concepts—to the tangible— the physical implementation of these concepts in real devices—was made possible through the development of data structures. Data structures enable computers to store, process, and retrieve vast amounts of information with precision and speed.
Data Structures: Organization and Efficiency
Data structures are specific methods of organizing and storing information in a computer’s memory to ensure efficient data access and management. Each data structure is designed for different applications, allowing for optimized performance in various computational tasks.
Fundamental Data Structures
- Arrays: One of the most basic data structures, where elements are stored in sequential memory locations. Arrays allow fast access to specific elements but are static, meaning their size cannot be easily changed.
- Linked Lists: A structure that stores data in noncontiguous memory locations, using pointers to connect elements. Linked lists offer flexibility for adding and removing elements but can be slower for searching operations.
- Trees: Hierarchical data structures in which data is organized into “nodes” with parent-child relationships. Trees are widely used for representing hierarchical relationships, such as file systems.
- Graphs: Used to model complex relationships, graphs represent data as nodes (vertices) connected by edges. They are fundamental in networking, AI, and many optimization problems.
John von Neumann’s Contribution
John von Neumann was one of the pioneers of modern computing and is best known for the von Neumann architecture, which introduced the concept that a computer should store both data and instructions in memory.
This principle simplified the design of computational systems and became the foundation of modern computers. Thanks to von
Neumann’s architecture, computers can store large amounts of data and execute programs more efficiently, without requiring manual input for each instruction.
Data Organization and Management: The Foundation of Technology
Data structures play a crucial role in efficient information management. The choice of an appropriate data structure depends on the nature of the application and the performance requirements.
A well-organized data system can significantly enhance computer performance, improving the speed of retrieval, processing, and storage of information.
Additionally, data structures allow computers to manage largescale datasets efficiently, whether in databases, artificial intelligence applications, or any system requiring fast data processing.
“Are You Smarter Than a Computer?” (20 minutes)

The role of algorithms and the contribution of Muhammad AlKhwarizmi to the development of mathematical science and programming are key to understanding the evolution of science. A detailed review of his work and its impact on modern problem-solving through algorithmic processes highlights the deep connection between mathematics, computer science, and artificial intelligence.
The Historical Legacy of Al-Khwarizmi
Muhammad Al-Khwarizmi (c. 780–850 AD) was one of the earliest mathematicians and astronomers of his time. He worked at the House of Wisdom (Bayt al-Hikma) in Baghdad, an academic and research centre that promoted mathematics, geometry, astronomy, and accounting. Here, many works of Greek and Indian mathematicians were translated, greatly influencing Al-Khwarizmi’s thinking.
One of his most important works, “Al-Kitab al-Mukhtasar fi
Hisab al-Jabr wal-Muqabala” (“The Compendious Book on Calculation by Completion and Balancing”) introduced a systematic method for solving equations, now known as algebra. The term “algebra” comes from the Arabic word “al-jabr”, which refers to the process of reconstructing and transforming equations.
However, Al-Khwarizmi’s most significant contribution was the development of the algorithmic method. The word “algorithm” is derived from his name and is used to describe a precise, step-by-step process for solving specific problems. His work on numerical methods also introduced the Indian numeral system (which later became known as Arabic numerals) and paved the way for the decimal number system.
What Are Algorithms?
Algorithms are fundamental problem-solving tools that are used not only in mathematics but across multiple disciplines and real-world applications. An algorithm is a predefined sequence of steps or instructions used to solve a problem or achieve a specific goal. Algorithms are not limited to numerical operations—they are applied in logic, engineering, artificial intelligence, and many other fields.
For example, sorting algorithms arrange data in a specific order
(e.g., numerical or alphabetical). One of the simplest sorting algorithms is Bubble Sort, which compares and swaps adjacent elements until they are in order. This step-by-step process is an example of how algorithms break down complex problems into manageable steps.
Al-Khwarizmi’s concept of an algorithm was revolutionary because it focused on logical analysis and breaking down complex problems into simpler steps. This methodology became the foundation of modern computational thinking, where problems are decomposed into smaller, more manageable parts.
Algorithms and Sorting
Sorting is one of the first and most important problems addressed in computer science. The purpose of sorting is to rearrange data based on a specific criterion, such as numerical or alphabetical order. Sorting algorithms are crucial for many applications, from database searches to big data analysis.
Some of the most well-known sorting algorithms include:
- Bubble Sort: Repeatedly compares and swaps elements that are out of order. Although simple, it is slow for large datasets.
- Selection Sort: Finds the smallest element and places it in the correct position, repeating the process for the remaining elements.
- Quick Sort: Recursively divides data into smaller parts, making it one of the fastest sorting algorithms.
These algorithms demonstrate problem decomposition, a method introduced by Al-Khwarizmi. The ability to organize and process information efficiently is one of the key principles of algorithmic thinking.
Algorithms in the Modern Era: Artificial Intelligence and Machine Learning
Today, algorithms have expanded beyond mathematics and programming into artificial intelligence (AI) and machine learning (ML). AI relies on algorithms that can learn and improve over time by analyzing patterns in data.
For example, neural networks are algorithms that mimic the human brain by processing complex patterns and recognizing relationships in large datasets. These systems use algorithmic processes to analyze massive amounts of data and make predictions or decisions.
The legacy of Al-Khwarizmi is evident even in these advanced modern applications. The way we analyze problems, write programs, and solve complex challenges is based on the fundamental principles he introduced over 1,000 years ago.
Conclusion
The legacy of Al-Khwarizmi is one of the most important in the history of mathematics and computer science. From developing algebra to introducing the concept of algorithms, his work shaped how we understand and solve problems. Today, algorithms remain at the core of science and technology, allowing us to build intelligent machines, analyze vast datasets, and manage complexity in the modern world.
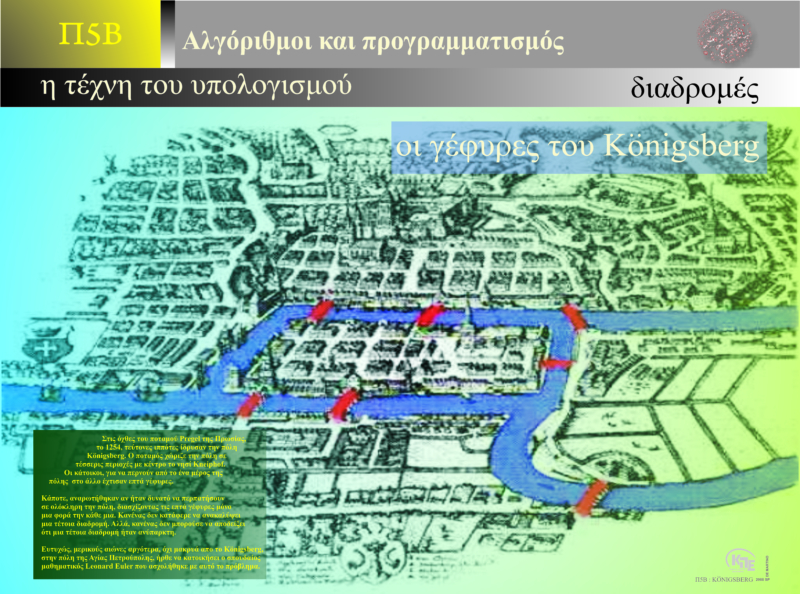
The solution to the Königsberg Bridges Problem by mathematician Leonhard Euler in 1736 is one of the most significant milestones in mathematical history. The city of Königsberg (now Kaliningrad) was divided by the Pregel River, creating two main land areas and two islands, all connected by seven bridges. The famous challenge at the time was:
Can a person take a walk that crosses each bridge exactly once without repeating any bridge?
At first glance, the problem seemed simple, yet its complexity led many to question whether such a route was actually possible. Numerous attempts were made through trial and error, but no one succeeded. Euler was the first to realize that the solution did not depend on the geography of the bridges, but rather on the underlying structure of the problem itself.
Euler’s Approach: From Geography to Abstraction
Euler approached the problem in a revolutionary way. Instead of focusing on the physical layout of the bridges and the islands, he represented the city’s structure using a graph:
- Each land area or island became a vertex (node).
- Each bridge became an edge (connection) between vertices.
With this graph representation, the problem could be reformulated as:
Is it possible to draw a path through the graph that passes through each edge exactly once?
This type of path is now known as an Eulerian path.
Euler’s Key Observation: The Role of Vertex Degree
Euler made a critical discovery:
For a continuous path to pass through each edge exactly once, each vertex must have an even number of edges (connections).
To understand this, consider what happens when a person enters and exits a landmass. For each entry, there must be a corresponding exit. Thus, an area with an odd number of connections would require an extra crossing, making it impossible to complete the walk without repeating a bridge.
Euler analyzed the graph of Königsberg and found that all four vertices had an odd number of connections. This proved that no such walk was possible.
Euler’s Conclusion and the Birth of Graph Theory
Euler’s final conclusion was that there is no solution to the Königsberg Bridges Problem. However, this realization had profound mathematical significance.
Euler’s work laid the foundation of graph theory, a mathematical framework that represents networks of interconnected objects. Today, graph theory is applied in fields such as:
- Computer Science (networking, data structures, and optimization)
- Social Networks (analyzing connections between individuals)
- Biology (mapping molecular interactions)
- Logistics & Transportation (efficient route planning)
- Artificial Intelligence (search algorithms and decision trees)
Eulerian Paths and Eulerian Circuits
Euler’s analysis led to the formal definition of Eulerian paths and circuits:
- A graph has an Eulerian path if it has exactly two vertices with an odd number of edges.
- A graph has an Eulerian circuit (a closed path passing through all edges exactly once) if all vertices have an even number of edges.
Euler’s abstract approach to the problem transformed mathematics, showing that graph theory could be used to analyze connectivity problems in an entirely new way.
Why This Problem Matters Today
Euler’s graph-based approach was revolutionary, as it introduced a new way of thinking about mathematical problems. His work was one of the first examples of using abstraction to solve realworld problems, leading to the development of discrete mathematics.
Graph theory is now a powerful tool in various fields, from mapping city roads to analyzing social networks and even understanding molecular structures in chemistry.
Euler’s insight that the structure of a problem matters more than its physical representation remains one of the most fundamental ideas in modern mathematics and science.

The Tower of Hanoi, also known as “Le Tour d’Hanoï” in French or Tower of Hanoi in English, is a classic mathematical puzzle and logic game, invented by the French mathematician Édouard Lucas in 1883. The puzzle involves moving disks from one tower (peg) to another, following a set of specific rules.


Algorithms and complexity are fundamental concepts in modern science, with applications ranging from mathematics and computer science to biology and physics. The study of algorithms provides a powerful tool for understanding how simple processes can lead to highly complex and organized behaviors. One of the most fascinating examples of this interaction is John Conway’s Game of Life, a cellular automaton that simulates system evolution based on simple rules.
What is an Algorithm?
An algorithm is a well-defined sequence of steps or rules applied to solve a problem or execute a process. While algorithms themselves are often simple, their application can lead to highly complex and unpredictable outcomes. This characteristic of “complexity” often emerges from the interaction of multiple simple components within a system, collectively creating rich and intricate structures.
Conway’s Game of Life: A Model for Complexity
The Game of Life is an example that illustrates how algorithms can generate complexity from simple rules. It is a cellular automaton where a grid of cells follows a set of three simple rules:
- A live cell dies if it has fewer than two or more than three live neighbors (underpopulation or overpopulation).
- A live cell survives if it has two or three live neighbors.
- A dead cell becomes alive if it has exactly three live neighbors (reproduction).
Despite their simplicity, these rules lead to an astonishing variety of patterns and behaviors. Some patterns remain stable, others oscillate, some move across the grid, while others disappear.
This demonstrates that even the simplest rules can give rise to extreme complexity, a key characteristic of complex systems.
Complexity in Natural Systems
The idea that simple rules can lead to complexity is not unique to computer science or mathematics. In nature, many seemingly complex processes can be explained by simple interaction rules.
Examples of Complexity in Nature
- Evolution by Natural Selection:
- Charles Darwin’s theory of evolution is based on a simple algorithm: organisms with advantageous traits survive and reproduce.
- Over millions of years, small interactions and random mutations have led to the enormous diversity of life we see today.
- Embryonic Development:
- A single cell (zygote) divides and differentiates
into a fully formed organism based on genetic algorithms. o The genetic code provides simple instructions that interact with the environment, resulting in highly complex biological structures, like the human body.
- Flocking Behavior in Animals:
- Schools of fish, flocks of birds, and swarms of insects follow three basic rules:
- Stay close to neighbors.
- Match speed with nearby individuals.
- Avoid collisions.
- These simple behavioral algorithms produce stunning, coordinated movements without a central leader.
- Schools of fish, flocks of birds, and swarms of insects follow three basic rules:
The Search for Algorithms in Science
The pursuit of new algorithms is a central effort in science, as researchers aim to understand and simulate complex systems.
- In computer science, algorithms process vast amounts of data, power artificial intelligence, and model realworld phenomena.
- In biology, genetic algorithms simulate evolution and help scientists understand biological adaptation.
- In physics, simulations of fluid dynamics and planetary motion rely on sophisticated numerical algorithms.
A notable example is the use of algorithms in machine learning, where computers learn patterns and behaviors from data, mirroring how natural systems evolve over time.
Complexity in Machine Learning and Artificial Intelligence
With the rise of artificial intelligence (AI) and machine learning (ML), algorithms play a central role in modeling complexity.
- Machine learning relies on algorithms that allow machines to “learn” from data and develop behaviors without explicit programming.
- Neural networks, inspired by the human brain, process vast amounts of complex information to recognize patterns and make predictions.
- AI systems, such as chatbots and autonomous vehicles, adapt through algorithmic feedback loops, improving over time.
Here, complexity is not just a natural phenomenon, but something that can be designed and engineered using algorithmic processes.
Conclusion
Algorithms and complexity are fundamental to understanding the world around us. From simple cellular automata like Conway’s Game of Life to highly complex natural and artificial systems, algorithms help us explore how simple interactions create rich and dynamic behaviors.
The search for new algorithms continues, as the study of complexity holds the key to unlocking the mysteries of life, evolution, and intelligence.

Algorithms are fundamental tools for solving complex problems, and the labyrinth is a powerful analogy that demonstrates how algorithms can be applied in real-world scenarios. A labyrinth represents a complex system of choices and pathways, symbolizing the need for exploration and strategic decision-making to find the optimal solution.
To better understand why algorithms are essential in solving such problems, let’s examine the key elements that make them so important.
What is Complexity?
In computational terms, complexity refers to how difficult a problem is to solve and the number of possible choices that must be explored to reach a solution. In the case of a labyrinth, complexity arises from the number of intersections, pathways, and potential dead ends. Similarly, in a computational problem, complexity relates to the size of data, conditions, and possible solutions that must be considered.
Algorithms are designed to manage complexity efficiently, allowing for a systematic search for the best solution instead of relying on random trial and error.
Exploration and Finding the Optimal Path
When trying to solve a problem similar to a labyrinth, the fundamental approach is searching for a solution. A search algorithm explores all possible paths until the correct one is found. This process can be executed in different ways, depending on the algorithm used.
Strategies for Searching in a Labyrinth
- Exhaustive Search (Brute Force) o A simple approach involves trying every possible path (brute-force search) until the correct one is found.
- While guaranteed to find a solution, this method is inefficient for problems with many choices, as it requires checking all possibilities one by one.
- Systematic Exploration (Breadth-First Search – BFS)
- A more organized approach involves exploring all nearby paths before moving further away.
- BFS ensures that the shortest path is found by systematically checking each level of choices before proceeding.
- Heuristic Search (A* Algorithm)
- Heuristic algorithms prioritize the most promising paths by estimating which ones are likely to be optimal.
- The A* algorithm, for example, evaluates each possible path’s estimated cost and chooses the one that seems most efficient.
- This method is widely used in pathfinding applications, such as GPS navigation.
Algorithms and Optimization
Optimization is a crucial goal when using algorithms to solve complex problems like labyrinths. Instead of simply finding any solution, the goal is often to find the best or most efficient solution in terms of time and cost.
For example, in a labyrinth, simply finding an exit may be enough, but in many real-world problems, the optimal solution is needed—such as the fastest or least resource-consuming path. Optimization algorithms help ensure that valuable time and resources are not wasted during the search.
Dijkstra’s Algorithm: Finding the Shortest Path
One of the most famous optimization algorithms is Dijkstra’s Algorithm, which is used to find the shortest path between two points.
- This algorithm systematically explores possible paths, always selecting the one with the lowest total cost.
- It is ideal for problems such as navigation in road networks, where finding the fastest route is critical.
Computational Complexity
Algorithms are not only evaluated based on their ability to find solutions but also on their computational complexity—how efficiently they scale as the problem size increases.
- A small labyrinth can be solved quickly with basic methods, but as the size of the problem grows, complexity increases.
- Computational complexity is measured in time (how many steps are required) and space (how much memory is used).
- Algorithms designed for large and complex problems must be efficient, ensuring they do not consume excessive resources and can produce results in a reasonable amount of time.
Real-World Applications of Algorithms
Algorithms are not just abstract mathematical concepts—they are applied in real-world problems, from GPS navigation to robotics and network systems.
- Navigation Systems (GPS & Google Maps) o Finding the shortest route between two locations is a pathfinding problem, much like solving a labyrinth.
- Search algorithms are used to find the best route while considering factors such as traffic, road closures, and speed limits.
- Artificial Intelligence & Machine Learning
o AI models search for patterns and optimal solutions within vast amounts of data.
- Many machine learning models “learn” through processes that resemble search algorithms, exploring various possibilities and choosing the most effective paths.
Conclusion
The analogy of the labyrinth with complexity problems is a powerful metaphor for understanding how algorithms work. By designing and applying search and optimization algorithms, we can systematically solve even highly complex problems.
From simple searches to advanced optimization techniques, algorithms help us find the correct path, no matter how intricate the problem may be. Whether navigating a physical maze, optimizing data processing, or training AI models, algorithms provide the most efficient way to handle complexity, ensuring the best solution in the shortest possible time.

Utilization
Placement optimization is a crucial challenge in many fields, from logistics and storage management to computational geometry and industrial planning. Finding the best way to arrange objects within a limited space can maximize efficiency, reduce costs, and minimize waste.
Algorithms provide the systematic and efficient methods needed to tackle these complex problems, helping to determine the best possible placement in various real-world scenarios.
What is Optimal Placement?
Optimal placement refers to arranging a set of objects within a constrained space in a way that maximizes space utilization. The goal is to fit as many objects as possible while avoiding wasted space or inefficient layouts.
This problem appears in various applications, such as:
- Warehouse Storage: Optimizing shelf space to store the maximum number of goods.
- Freight Loading: Efficiently arranging cargo in trucks, ships, or airplanes to minimize transportation costs.
- Product Packaging: Organizing items within containers or boxes to reduce packaging waste and increase efficiency.
Complexity of Placement Problems
The difficulty in solving placement optimization problems arises from multiple factors:
- Objects may have different sizes and shapes (e.g., irregularly shaped items in a warehouse).
- The available space may have restrictions (e.g., fixed dimensions or weight limits).
- Gaps and wasted space should be minimized to maximize efficiency.
- Multiple parametres must be considered simultaneously, such as cost, accessibility, and environmental constraints.
The challenge is not just finding a solution but identifying the best solution, meaning maximizing space utilization while minimizing costs and inefficiencies.
Algorithms for Placement Optimization
To handle the complexity of space allocation problems, various algorithmic approaches have been developed. Each algorithm is suited for different types of problems and constraints.
Packing Algorithms
Packing algorithms focus on fitting objects into a limited space while minimizing gaps and maximizing efficiency. One well-known example is the box-packing problem, where items of various sizes must be arranged inside a container.
Variations of the problem include:
- 2D Packing (e.g., arranging rectangles in a warehouse or placing graphics on a screen).
- 3D Packing (e.g., optimizing space in cargo containers).
- Irregular Packing (e.g., arranging uniquely shaped parts in manufacturing).
Bin Packing Algorithm
The Bin Packing problem aims to fit a set of items into a minimal number of containers (bins) while respecting space or weight constraints.
Applications include:
- Inventory management (optimizing stock allocation).
- Transportation logistics (maximizing load efficiency).
- Computing and memory allocation (efficient use of storage or processing resources).
Heuristic Algorithms
For complex placement problems, where exhaustive search is impractical, heuristic methods provide good solutions in a reasonable time.
Examples include:
- Genetic Algorithms (GA): Mimic natural selection to iteratively improve placement solutions.
- Simulated Annealing (SA): Inspired by metal cooling, this method allows controlled randomness to explore better configurations.
- Greedy Algorithms: Make locally optimal choices at each step to build an overall efficient solution.
While these methods do not always guarantee the absolute best placement, they offer efficient solutions for large-scale problems.
Linear Programming for Optimization
For high-precision solutions, linear programming is used to mathematically model the placement problem using equations and constraints.
Applications include:
- Production planning (allocating factory resources optimally).
- Supply chain management (balancing cost and storage efficiency).
- Transport networks (optimizing package deliveries).
Challenges and Computational Complexity
The main challenge in placement optimization is its computational complexity.
- As the number of objects increases, the number of possible placements grows exponentially.
- Finding the absolute best placement is often NPhard, meaning it becomes computationally infeasible for large datasets.
- Efficient solutions require balancing accuracy with computation time, making heuristic and approximation methods essential.
Real-World Applications of Placement Optimization
Placement optimization is used in various industries and daily life, including:
- Industrial & Warehouse Management
- Maximizing storage space in distribution centers.
- Improving the layout of assembly lines.
- Reducing handling time and costs.
- Transportation & Logistics
- Efficiently loading trucks, ships, and airplanes.
- Minimizing fuel consumption and travel costs.
- Enhancing route planning for deliveries.
- Everyday Life Applications
- Packing suitcases for travel efficiently.
- Optimizing furniture arrangements in a home or office.
- Organizing digital storage (e.g., file compression and memory management).
Conclusion
Placement optimization is a crucial problem with widespread applications, from logistics and industry to personal organization.
Algorithms help maximize efficiency, reduce waste, and save costs, making them indispensable in a resource-limited world. As these problems grow in complexity, heuristic methods, machine learning, and optimization algorithms continue to evolve, enabling even better solutions for efficient space utilization.
«Digital Artists» (20 λεπτά)

Digitization is the process of converting analog information into a digital format, making it understandable and manageable by computational systems. The transition from analog to digital has transformed communication, entertainment, art, science, and industry, making information more flexible, accessible, and costeffective to store, process, and transmit.
Analog vs. Digital: Key Differences
To fully understand digitization, we must first differentiate between analog and digital information.
Analog Information
- Continuous and smoothly varying over time.
- Represents physical properties such as sound, light, or motion.
- Unlimited values with no discrete steps (e.g., sound waves in vinyl records or radio signals).
- Sensitive to degradation from noise, environmental conditions, or ageing (e.g., film deterioration, magnetic tape wear).
Digital Information
- Discrete, represented in binary form (0s and 1s).
- Precisely recorded, stored, and transmitted without quality loss.
- Composed of data units, such as pixels in images or bits in audio files.
- Easily processed, edited, and shared without deterioration over time.
The Process of Digitization
Digitization involves two main steps:
- Sampling o The analog signal is measured at discrete time
intervals.
o The more samples taken, the more accurately the digital version represents the original.
- Quantization o Each sample’s value is rounded to the nearest
digital representation. o Higher bit-depth results in greater accuracy and finer detail preservation.
For example, in digital audio, increasing the sampling rate (e.g., 44.1 kHz in CDs) and bit-depth (e.g., 16-bit or 24-bit) improves sound fidelity.
Digital Images and Pixels
One of the most common examples of digitization is digital imaging. When an image is digitized, it is broken down into a grid of tiny units called pixels.
- Each pixel stores color and brightness information in numerical form.
- A higher pixel density (resolution) results in a more detailed image.
- Example: A high-resolution photograph contains millions of pixels that recreate fine details accurately.
Advantages of Digitization
- Storage and Retrieval
- Digital data can be stored indefinitely without quality loss.
- Unlike analog formats (which degrade over time), digital data remains unchanged no matter how many times it is copied or accessed.
- Precision and Clarity
- Digital files maintain consistent quality and are resistant to interference (e.g., digital music retains sound clarity, unlike worn-out cassette tapes).
- Easy Editing and Processing
- Digital content (images, audio, video, text) can be edited, enhanced, and manipulated using software.
- Fast Transmission and Sharing
- Digital files can be transmitted instantly across networks (e.g., streaming services, online documents).
- Example: YouTube and streaming platforms allow videos to reach global audiences in seconds.
- Security and Protection
- Encryption and backup systems ensure data integrity and protect against unauthorized access.
Applications of Digitization
- Digital Photography and Art
- Preserves historical artworks in high fidelity.
- Allows artists to create digital masterpieces with graphic design tools.
- Digital Music and Audio
- Audio recordings are stored in MP3, WAV, FLAC
- Enables instant access to music libraries worldwide. Video and Cinema
- Movies are now digitally edited, produced, and streamed.
- Enhances special effects, animation, and postproduction efficiency.
- Document Archiving and Scanning
- Physical books and records can be scanned and stored digitally for easy retrieval and distribution.
Conclusion
Digitization is a cornerstone of modern technology, enabling efficient storage, sharing, and processing of information. By converting analog data into digital formats, it enhances accessibility, security, and usability, revolutionizing how we work, communicate, and create in the digital era.
«Inside a Robot’s Imagination» (20 λεπτά)

Artificial Intelligence: Definition and Applications
The term “artificial intelligence” refers to the branch of computer science that deals with the design and implementation of computational systems that mimic aspects of human behavior, which imply even minimal intelligence, such as learning, adaptability, inference, contextual understanding, problem-solving, and more.
Artificial intelligence represents a convergence point between multiple sciences such as computer science, psychology, philosophy, engineering, and others, aiming to synthesize intelligent behavior, incorporating reasoning, learning, and environmental adaptation. AI is applied both in machines and specially designed computers and is divided into two categories:
1) Symbolic Artificial Intelligence: which attempts to simulate human intelligence algorithmically using symbols and high-level logical rules.
2) Subsymbolic Artificial Intelligence: which reproduces human intelligence using basic numerical models that inductively compose intelligent behaviors through successive simpler building blocks.
Depending on its specific scientific goal, artificial intelligence is also categorized into various fields such as problem-solving, machine learning, knowledge discovery, knowledge systems, and more. It can also be combined with other fields such as computer vision and robotics, which are independent areas of its application.
The most impressive and globally known application of artificial intelligence is the humanoid “robot Sophia.” It was created in 2016 by Professor David Hanson (owner of the company Hanson Robotics) and is the first robot that managed to mimic human behavior, express emotions, and engage in conversation with people. It can speak more than 20 languages, including Greek.



