“Three Millennia of Logic” (60 minutes)

“A Wonderful Company” (80 minutes)

In 1645, the French mathematician Blaise Pascal built the first true mechanical calculator, known as the Pascaline. The Pascaline was capable of performing relatively simple mathematical calculations. This small-sized machine consisted of pulleys that, when rotated by the user, displayed the results. The original “computer” had five gears, allowing calculations with relatively small numbers, but later versions were built with six and eight gears. This machine could perform only two operations: addition and subtraction.

At the top of the Pascaline, there was a row of toothed wheels, known as gears, each containing the numbers from 0 to 9. The first wheel represented units, the second tens, the third hundreds, and so on.

In 1673, the mathematician and philosopher Gottfried Wilhelm

Leibniz (1646-1716) improved Pascal’s machine by creating a manual calculating machine that could perform multiplication and division besides addition and subtraction. During the early stages of his career, Leibniz also invented the binary number system (0 and 1), which remains the foundation of modern computer programming languages. This machine is currently preserved in a technical museum in Germany.

The English mathematician, philosopher, and logician George Boole (1815–1864), through his two works:

  • “The Mathematical Analysis of Logic” (1847)
  • “An Investigation of the Laws of Thought on Which the Mathematical Theories of  Logic and Probabilities” (1854)

transformed propositional logic into an algebraic system, known as Boolean Algebra, which operates on the set B = , equipped with the operations “+” (OR) and “•” (AND).

Boolean Logic and Aristotelian Logic

Aristotelian logic, which states that “it is impossible for the same property to belong and not belong to the same object” (principle of contradiction), is translated in Boolean Algebra as “nothing can simultaneously belong and not belong to a given class.”

Boole’s system was built upon the principles of classical algebra, but with a very specific structure. Unlike elementary algebra, where variables take numerical values and the main operations are addition and multiplication, Boolean Algebra uses only two values, “1” and “0”. Additionally, it introduces three fundamental operations:

  • Conjunction (“Λ”) (AND)
  • Disjunction (“V”) (OR)
  • Negation (“-“) (NOT)

Boolean algebra forms the foundation of modern digital circuits and computer logic, making it essential in computer science and programming.

Friedrich Ludwig Gottlob Frege (1848–1925) and the Foundations of Modern Programming Languages

Friedrich Ludwig Gottlob Frege was a German mathematician, logician, and philosopher who laid the foundation for modern programming languages.

His work in logic, the philosophy of mathematics, philosophical logic, and the theory of meaning became the starting point and reference for subsequent research in these fields. Frege introduced a symbolic logic system that significantly extended Aristotelian logic and attempted to reduce arithmetic to logic, demonstrating that arithmetic propositions are analytic. He also introduced two central concepts in the theory of meaning: sense (“Sinn”) and reference (“Bedeutung”).

Frege’s Theory of Meaning

Frege’s research in the theory of meaning originated from his pursuit of a conceptual notation system for pure thought, which would allow for the most reliable verification of logical reasoning and reveal all hidden assumptions involved in arguments.

This symbolic system aimed to realize Leibniz’s ideal of a universal language, a formal system in which logical validity could be objectively determined. Within this framework, Frege distinguished between sense and reference, separating linguistic meaning from subjective mental representations and psychological events.

Frege’s theory of meaning is based on this distinction between sense and reference and was developed in response to:

  1. The rejection of a simplistic representational view of meaning, which assumes that meaning is merely a link between words and objects.
  2. The rejection of psychologism, the idea that meaning is a psychological entity and that logical relationships are merely psychological associations.

According to Frege, the meaning of a linguistic expression is not simply a direct association between the expression and an object, nor is it merely a mental image or representation. Instead, meaning is an abstract, logical structure that determines how expressions relate to one another within a formal system.

Impact on Computer Science and Logic

Frege’s contributions laid the groundwork for modern formal logic, which in turn influenced computer science, artificial intelligence, and programming language theory. His formalization of logic inspired the development of predicate logic, which serves as the foundation for automated reasoning, computational logic, and programming languages today.

“Two Numbers Are More Than Enough” (20 minutes)

The Transition to Technology – From Abstract to Tangible – Data Structures and Organization (Δομές δεδομένων)

In modern computer technology, the organization of data is fundamental to the efficient operation of systems. The transition from the abstract—the logical and mathematical concepts—to the tangible— the physical implementation of these concepts in real devices—was made possible through the development of data structures. Data structures enable computers to store, process, and retrieve vast amounts of information with precision and speed.

Data Structures: Organization and Efficiency

Data structures are specific methods of organizing and storing information in a computer’s memory to ensure efficient data access and management. Each data structure is designed for different applications, allowing for optimized performance in various computational tasks.

Fundamental Data Structures

  • Arrays: One of the most basic data structures, where elements are stored in sequential memory locations. Arrays allow fast access to specific elements but are static, meaning their size cannot be easily changed.
  • Linked Lists: A structure that stores data in noncontiguous memory locations, using pointers to connect elements. Linked lists offer flexibility for adding and removing elements but can be slower for searching operations.
  • Trees: Hierarchical data structures in which data is organized into “nodes” with parent-child relationships. Trees are widely used for representing hierarchical relationships, such as file systems.
  • Graphs: Used to model complex relationships, graphs represent data as nodes (vertices) connected by edges. They are fundamental in networking, AI, and many optimization problems.

John von Neumann’s Contribution

John von Neumann was one of the pioneers of modern computing and is best known for the von Neumann architecture, which introduced the concept that a computer should store both data and instructions in memory.

This principle simplified the design of computational systems and became the foundation of modern computers. Thanks to von

Neumann’s architecture, computers can store large amounts of data and execute programs more efficiently, without requiring manual input for each instruction.

Data Organization and Management: The Foundation of Technology

Data structures play a crucial role in efficient information management. The choice of an appropriate data structure depends on the nature of the application and the performance requirements.

A well-organized data system can significantly enhance computer performance, improving the speed of retrieval, processing, and storage of information.

Additionally, data structures allow computers to manage largescale datasets efficiently, whether in databases, artificial intelligence applications, or any system requiring fast data processing.

“Are You Smarter Than a Computer?” (100 minutes)

The role of algorithms and the contribution of Muhammad AlKhwarizmi to the development of mathematical science and programming are key to understanding the evolution of science. A detailed review of his work and its impact on modern problem-solving through algorithmic processes highlights the deep connection between mathematics, computer science, and artificial intelligence.

The Historical Legacy of Al-Khwarizmi

Muhammad Al-Khwarizmi (c. 780–850 AD) was one of the earliest mathematicians and astronomers of his time. He worked at the House of Wisdom (Bayt al-Hikma) in Baghdad, an academic and research centre that promoted mathematics, geometry, astronomy, and accounting. Here, many works of Greek and Indian mathematicians were translated, greatly influencing Al-Khwarizmi’s thinking.

One of his most important works, “Al-Kitab al-Mukhtasar fi

Hisab al-Jabr wal-Muqabala” (“The Compendious Book on Calculation by Completion and Balancing”) introduced a systematic method for solving equations, now known as algebra. The term “algebra” comes from the Arabic word “al-jabr”, which refers to the process of reconstructing and transforming equations.

However, Al-Khwarizmi’s most significant contribution was the development of the algorithmic method. The word “algorithm” is derived from his name and is used to describe a precise, step-by-step process for solving specific problems. His work on numerical methods also introduced the Indian numeral system (which later became known as Arabic numerals) and paved the way for the decimal number system.

What Are Algorithms?

Algorithms are fundamental problem-solving tools that are used not only in mathematics but across multiple disciplines and real-world applications. An algorithm is a predefined sequence of steps or instructions used to solve a problem or achieve a specific goal. Algorithms are not limited to numerical operations—they are applied in logic, engineering, artificial intelligence, and many other fields.

For example, sorting algorithms arrange data in a specific order

(e.g., numerical or alphabetical). One of the simplest sorting algorithms is Bubble Sort, which compares and swaps adjacent elements until they are in order. This step-by-step process is an example of how algorithms break down complex problems into manageable steps.

Al-Khwarizmi’s concept of an algorithm was revolutionary because it focused on logical analysis and breaking down complex problems into simpler steps. This methodology became the foundation of modern computational thinking, where problems are decomposed into smaller, more manageable parts.

Algorithms and Sorting

Sorting is one of the first and most important problems addressed in computer science. The purpose of sorting is to rearrange data based on a specific criterion, such as numerical or alphabetical order. Sorting algorithms are crucial for many applications, from database searches to big data analysis.

Some of the most well-known sorting algorithms include:

  • Bubble Sort: Repeatedly compares and swaps elements that are out of order. Although simple, it is slow for large datasets.
  • Selection Sort: Finds the smallest element and places it in the correct position, repeating the process for the remaining elements.
  • Quick Sort: Recursively divides data into smaller parts, making it one of the fastest sorting algorithms.

These algorithms demonstrate problem decomposition, a method introduced by Al-Khwarizmi. The ability to organize and process information efficiently is one of the key principles of algorithmic thinking.

Algorithms in the Modern Era: Artificial Intelligence and Machine Learning

Today, algorithms have expanded beyond mathematics and programming into artificial intelligence (AI) and machine learning (ML). AI relies on algorithms that can learn and improve over time by analyzing patterns in data.

For example, neural networks are algorithms that mimic the human brain by processing complex patterns and recognizing relationships in large datasets. These systems use algorithmic processes to analyze massive amounts of data and make predictions or decisions.

The legacy of Al-Khwarizmi is evident even in these advanced modern applications. The way we analyze problems, write programs, and solve complex challenges is based on the fundamental principles he introduced over 1,000 years ago.

Conclusion

The legacy of Al-Khwarizmi is one of the most important in the history of mathematics and computer science. From developing algebra to introducing the concept of algorithms, his work shaped how we understand and solve problems. Today, algorithms remain at the core of science and technology, allowing us to build intelligent machines, analyze vast datasets, and manage complexity in the modern world.

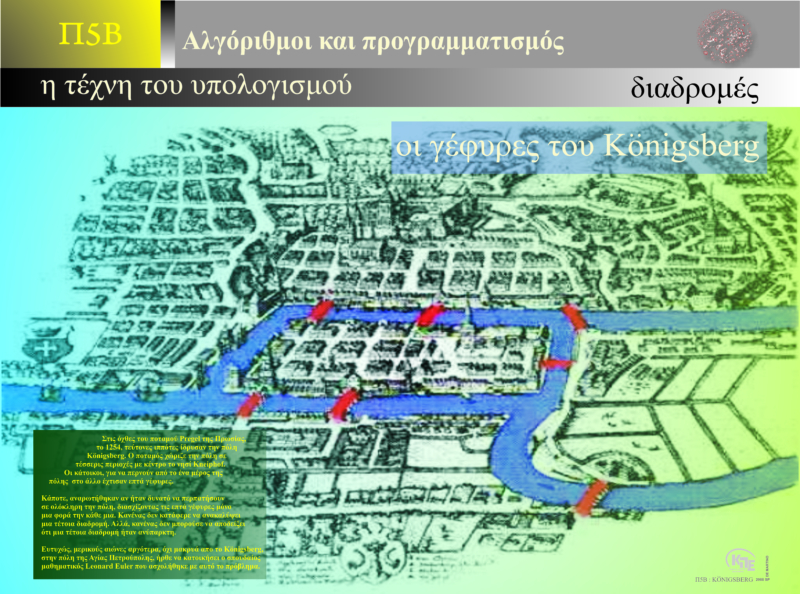
The solution to the Königsberg Bridges Problem by mathematician Leonhard Euler in 1736 is one of the most significant milestones in mathematical history. The city of Königsberg (now Kaliningrad) was divided by the Pregel River, creating two main land areas and two islands, all connected by seven bridges. The famous challenge at the time was:

Can a person take a walk that crosses each bridge exactly once without repeating any bridge?

At first glance, the problem seemed simple, yet its complexity led many to question whether such a route was actually possible. Numerous attempts were made through trial and error, but no one succeeded. Euler was the first to realize that the solution did not depend on the geography of the bridges, but rather on the underlying structure of the problem itself.

Euler’s Approach: From Geography to Abstraction

Euler approached the problem in a revolutionary way. Instead of focusing on the physical layout of the bridges and the islands, he represented the city’s structure using a graph:

  • Each land area or island became a vertex (node).
  • Each bridge became an edge (connection) between vertices.

With this graph representation, the problem could be reformulated as:

Is it possible to draw a path through the graph that passes through each edge exactly once?

This type of path is now known as an Eulerian path.

Euler’s Key Observation: The Role of Vertex Degree

Euler made a critical discovery:

For a continuous path to pass through each edge exactly once, each vertex must have an even number of edges (connections).

To understand this, consider what happens when a person enters and exits a landmass. For each entry, there must be a corresponding exit. Thus, an area with an odd number of connections would require an extra crossing, making it impossible to complete the walk without repeating a bridge.

Euler analyzed the graph of Königsberg and found that all four vertices had an odd number of connections. This proved that no such walk was possible.

Euler’s Conclusion and the Birth of Graph Theory

Euler’s final conclusion was that there is no solution to the Königsberg Bridges Problem. However, this realization had profound mathematical significance.

Euler’s work laid the foundation of graph theory, a mathematical framework that represents networks of interconnected objects. Today, graph theory is applied in fields such as:

  • Computer Science (networking, data structures, and optimization)
  • Social Networks (analyzing connections between individuals)
  • Biology (mapping molecular interactions)
  • Logistics & Transportation          (efficient   route planning)
  • Artificial Intelligence (search       algorithms          and decision trees)

Eulerian Paths and Eulerian Circuits

Euler’s analysis led to the formal definition of Eulerian paths and circuits:

  • A graph has an Eulerian path if it has exactly two vertices with an odd number of edges.
  • A graph has an Eulerian circuit (a closed path passing through all edges exactly once) if all vertices have an even number of edges.

Euler’s abstract approach to the problem transformed mathematics, showing that graph theory could be used to analyze connectivity problems in an entirely new way.

Why This Problem Matters Today

Euler’s graph-based approach was revolutionary, as it introduced a new way of thinking about mathematical problems. His work was one of the first examples of using abstraction to solve realworld problems, leading to the development of discrete mathematics.

Graph theory is now a powerful tool in various fields, from mapping city roads to analyzing social networks and even understanding molecular structures in chemistry.

Euler’s insight that the structure of a problem matters more than its physical representation remains one of the most fundamental ideas in modern mathematics and science.

The Tower of Hanoi, also known as “Le Tour d’Hanoï” in French or Tower of Hanoi in English, is a classic mathematical puzzle and logic game, invented by the French mathematician Édouard Lucas in 1883. The puzzle involves moving disks from one tower (peg) to another, following a set of specific rules.

Οι αλγόριθμοι και η πολυπλοκότητα αποτελούν κεντρικές έννοιες στη σύγχρονη επιστήμη, με εφαρμογές που επεκτείνονται από τα μαθηματικά και την πληροφορική έως τη βιολογία και τη φυσική. Για να κατανοήσουμε καλύτερα πώς οι απλές διαδικασίες μπορούν να οδηγήσουν σε εξαιρετικά πολύπλοκες και οργανωμένες συμπεριφορές, η μελέτη των αλγορίθμων έχει αναδειχθεί ως ένα από τα πιο ισχυρά εργαλεία. Ένα από τα πιο ενδεικτικά παραδείγματα αυτής της αλληλεπίδρασης είναι το “Παιχνίδι της Ζωής” του John Conway, ένα είδος κυψελοειδούς αυτόματου (cellular automaton) που προσομοιώνει την εξέλιξη ενός συστήματος βασισμένου σε απλούς κανόνες.

Τι είναι ένας αλγόριθμος;

Ο αλγόριθμος είναι μια σειρά καλά καθορισμένων κανόνων ή βημάτων που εφαρμόζονται για την επίλυση ενός προβλήματος ή την εκτέλεση μιας διαδικασίας. Στη ρίζα του, οι αλγόριθμοι είναι απλοί, ωστόσο η εφαρμογή τους μπορεί να οδηγήσει σε πολύπλοκα και μη προβλέψιμα αποτελέσματα. Αυτός ο χαρακτηρισμός της «πολυπλοκότητας» αφορά συχνά την αλληλεπίδραση πολλών απλών στοιχείων ή παραγόντων μέσα σε ένα σύστημα, τα οποία δημιουργούν συλλογικά πλούσιες και πολύπλοκες δομές.

Το “Παιχνίδι της Ζωής” του Conway: Ένα παράδειγμα πολυπλοκότητας

Το “Παιχνίδι της Ζωής” είναι ένα παράδειγμα που δείχνει πώς οι αλγόριθμοι μπορούν να γεννήσουν πολυπλοκότητα μέσα από απλούς κανόνες. Το παιχνίδι αυτό είναι ένα κυψελοειδές αυτόματο όπου ένα πλέγμα κυττάρων μπορεί να βρίσκεται σε δύο καταστάσεις: “ζωντανό” ή “νεκρό”. Οι κανόνες που ορίζουν την εξέλιξη του συστήματος είναι εξαιρετικά απλοί:

  1. Ένα ζωντανό κύτταρο πεθαίνει εάν έχει λιγότερους από δύο ή περισσότερους από τρεις ζωντανούς γείτονες (υπερπληθυσμός ή μοναξιά).
  2. Ένα ζωντανό κύτταρο επιβιώνει εάν έχει δύο ή τρεις ζωντανούς γείτονες.
  3. Ένα νεκρό κύτταρο ξαναγεννιέται εάν έχει ακριβώς τρεις ζωντανούς γείτονες.

Αυτοί οι τρεις κανόνες είναι η βάση για τη δημιουργία εκπληκτικής ποικιλίας προτύπων και δομών, ορισμένα από τα οποία παραμένουν σταθερά, άλλα αναπαράγονται ή κινούνται στο χώρο, ενώ ορισμένα εξαφανίζονται. Αυτό που κάνει το “Παιχνίδι της Ζωής” τόσο ενδιαφέρον είναι ότι από την απλότητα των κανόνων του προκύπτει εξαιρετικά πλούσια συμπεριφορά, μια ένδειξη της φύσης των πολύπλοκων συστημάτων.

Πολυπλοκότητα και Φυσικά Συστήματα

Η ιδέα ότι απλοί κανόνες μπορούν να οδηγήσουν σε πολυπλοκότητα δεν είναι αποκλειστική για την πληροφορική ή τα μαθηματικά. Στη φύση, πολλές διαδικασίες που φαίνονται περίπλοκες μπορούν να εξηγηθούν από απλούς κανόνες αλληλεπίδρασης. Για παράδειγμα, η εξέλιξη των ειδών μέσω φυσικής επιλογής, όπως περιγράφεται από τον Δαρβίνο, βασίζεται σε έναν απλό αλγόριθμο: τα ζώα με τα καλύτερα χαρακτηριστικά επιβιώνουν και αναπαράγονται. Ωστόσο, μέσα από εκατομμύρια χρόνια αλληλεπιδράσεων και μεταλλάξεων, αυτός ο κανόνας έχει οδηγήσει σε έναν τεράστιο πλούτο ζωής με αμέτρητα διαφορετικά είδη.

Παρομοίως, η ανάπτυξη ενός εμβρύου από ένα απλό κύτταρο σε έναν πλήρως λειτουργικό οργανισμό βασίζεται σε γενετικούς αλγόριθμους. Τα γονίδια, που περιέχουν τις πληροφορίες για τη δημιουργία και τη λειτουργία ενός οργανισμού, καθορίζουν μια σειρά απλών οδηγιών, οι οποίες αλληλεπιδρούν με το περιβάλλον και τα άλλα κύτταρα για να οδηγήσουν σε εξαιρετικά πολύπλοκες δομές, όπως το ανθρώπινο σώμα.

Η Αναζήτηση Αλγορίθμων στην Επιστήμη

Η αναζήτηση αλγορίθμων είναι μια από τις βασικές προσπάθειες στην επιστήμη, καθώς οι ερευνητές προσπαθούν να κατανοήσουν πώς λειτουργούν τα συστήματα και πώς μπορούν να προσομοιωθούν ή να αναπαραχθούν. Στην πληροφορική, οι αλγόριθμοι χρησιμοποιούνται για την επεξεργασία τεράστιων ποσοτήτων δεδομένων, για την ανάπτυξη τεχνητής νοημοσύνης και για τη μοντελοποίηση φυσικών φαινομένων. Η ανάπτυξη νέων αλγορίθμων επιτρέπει στους επιστήμονες να κατανοούν καλύτερα τη δομή των δεδομένων, να αναγνωρίζουν προτύπα και να προβλέπουν μελλοντικές συμπεριφορές.

Ένας άλλος τομέας όπου η αναζήτηση αλγορίθμων είναι ζωτικής σημασίας είναι η μοντελοποίηση της ζωής και της εξέλιξης. Οι αλγόριθμοι που χρησιμοποιούνται σε προσομοιώσεις της βιολογίας και της εξέλιξης μπορούν να βοηθήσουν στην κατανόηση των μηχανισμών που διέπουν τη ζωή και την πολυπλοκότητα. Για παράδειγμα, οι γενετικοί αλγόριθμοι, που μιμούνται τη διαδικασία της φυσικής επιλογής, χρησιμοποιούνται ευρέως στην επιστήμη των υπολογιστών για τη βελτιστοποίηση και την επίλυση προβλημάτων.

Η Πολυπλοκότητα στη Ζωή και στη Μηχανική Μάθηση

Σήμερα, με την άνοδο της τεχνητής νοημοσύνης και της μηχανικής μάθησης, οι αλγόριθμοι παίζουν καθοριστικό ρόλο στην κατανόηση της πολυπλοκότητας. Η μηχανική μάθηση βασίζεται σε αλγόριθμους που επιτρέπουν στα μηχανήματα να “μαθαίνουν” από τα δεδομένα και να αναπτύσσουν μοτίβα ή συμπεριφορές που προκύπτουν από σύνθετες αλληλεπιδράσεις. Εδώ, η πολυπλοκότητα δεν είναι μόνο ένα φυσικό φαινόμενο, αλλά κάτι που μπορεί να δημιουργηθεί από αλγοριθμικές διαδικασίες, δίνοντάς μας νέα εργαλεία για την επίλυση προβλημάτων που προηγουμένως θεωρούνταν άλυτα.

Συμπέρασμα

Οι αλγόριθμοι και η πολυπλοκότητα είναι θεμελιώδη στοιχεία για την κατανόηση του κόσμου γύρω μας. Από τα απλά κυψελοειδή αυτόματα όπως το “Παιχνίδι της Ζωής” έως τα εξαιρετικά περίπλοκα φυσικά συστήματα, οι αλγόριθμοι μας επιτρέπουν να δούμε πώς η αλληλεπίδραση απλών κανόνων μπορεί να δημιουργήσει την πολυπλοκότητα της φύσης. Η αναζήτηση νέων αλγορίθμων συνεχίζεται, καθώς η κατανόηση της πολυπλοκότητας είναι το κλειδί για να ξεκλειδώσουμε τα μυστικά της ζωής, της εξέλιξης και της ίδιας της ύπαρξης.

Οι αλγόριθμοι αποτελούν τα θεμελιώδη εργαλεία για την επίλυση προβλημάτων που εμπλέκουν πολυπλοκότητα, και ο λαβύρινθος είναι μια εξαιρετική αναλογία που δείχνει πώς οι αλγόριθμοι μπορούν να εφαρμοστούν στην πράξη. Ο λαβύρινθος απεικονίζει ένα πολύπλοκο σύστημα επιλογών και διαδρομών, που αντιπροσωπεύει την ανάγκη για εξερεύνηση και δοκιμή διαφορετικών στρατηγικών για να βρεθεί η βέλτιστη λύση.

Ας εξετάσουμε πιο λεπτομερώς τα βασικά στοιχεία που κάνουν έναν αλγόριθμο τόσο σημαντικό για την επίλυση τέτοιων προβλημάτων.

  1. Τι είναι η πολυπλοκότητα;

Η πολυπλοκότητα σε ένα πρόβλημα αναφέρεται στο πόσο δύσκολο είναι να λυθεί, καθώς και στο πλήθος των επιλογών που πρέπει να εξεταστούν προκειμένου να φτάσει κανείς στη λύση. Στην περίπτωση ενός λαβύρινθου, η πολυπλοκότητα προκύπτει από το πλήθος των διασταυρώσεων, των διαδρόμων και των πιθανών αδιεξόδων. Παρόμοια, σε ένα υπολογιστικό πρόβλημα, η πολυπλοκότητα σχετίζεται με την επεξεργασία μεγάλων όγκων δεδομένων, πολλών συνθηκών και πιθανών λύσεων που πρέπει να εξεταστούν.

Οι αλγόριθμοι είναι ουσιαστικά σχεδιασμένοι να διαχειρίζονται αυτή την πολυπλοκότητα, καθώς επιτρέπουν τη συστηματική αναζήτηση της καλύτερης λύσης χωρίς να χρειάζεται να δοκιμάζονται όλες οι επιλογές τυχαία.

  1. Διερεύνηση και Εύρεση Βέλτιστης Διαδρομής

Όταν προσπαθούμε να λύσουμε ένα πρόβλημα που μοιάζει με λαβύρινθο, η βασική στρατηγική είναι η αναζήτηση. Ένας αλγόριθμος αναζήτησης διερευνά όλες τις πιθανές διαδρομές μέχρι να βρει τη σωστή. Αυτή η διαδικασία μπορεί να γίνει με διάφορους τρόπους, ανάλογα με τον αλγόριθμο που χρησιμοποιείται.

Οι πιο βασικές στρατηγικές που χρησιμοποιούνται σε τέτοιες καταστάσεις είναι:

– Εξάντληση των επιλογών: Στην πιο απλή περίπτωση, ένας αλγόριθμος μπορεί να δοκιμάσει κάθε πιθανή διαδρομή (δηλαδή εξαντλητική αναζήτηση), μέχρι να βρει τη σωστή. Αυτός ο τρόπος, όμως, μπορεί να είναι πολύ αργός για προβλήματα με πολλές επιλογές, καθώς χρειάζεται να ελεγχθούν όλες οι διαδρομές μία προς μία.

– Συστηματική προσέγγιση: Ένας αλγόριθμος μπορεί να εφαρμόσει μια πιο συστηματική μέθοδο, όπως την εξερεύνηση όλων των διαδρομών κοντά στο σημείο εκκίνησης πριν προχωρήσει σε πιο απομακρυσμένα μονοπάτια. Αυτό γίνεται με αλγορίθμους όπως η ευρεία αναζήτηση (BFS), που εγγυάται ότι θα βρεθεί η συντομότερη διαδρομή.

– Αλγοριθμική προσέγγιση με προγνωστικές ενδείξεις: Οι αλγόριθμοι που χρησιμοποιούν ευρετική προσέγγιση, όπως ο Α, επιταχύνουν τη διαδικασία αναζήτησης αξιολογώντας ποια διαδρομή είναι πιθανό να είναι η καλύτερη. Αυτή η προσέγγιση συνδυάζει την έρευνα και τη λήψη αποφάσεων, δίνοντας προτεραιότητα στα μονοπάτια που φαίνονται πιο αποδοτικά.

  1. Αλγόριθμοι και Βελτιστοποίηση

Η βελτιστοποίηση είναι ένας σημαντικός στόχος όταν εφαρμόζουμε αλγόριθμους σε προβλήματα πολυπλοκότητας, όπως οι λαβύρινθοι. Δεν αρκεί απλώς να βρούμε μια λύση· συχνά αναζητούμε τη **βέλτιστη** λύση, δηλαδή την καλύτερη ή πιο αποδοτική από πλευράς χρόνου και κόστους.

Για παράδειγμα, σε έναν λαβύρινθο, η απλή εύρεση της εξόδου μπορεί να είναι αρκετή, αλλά σε πολλά προβλήματα, η βέλτιστη λύση περιλαμβάνει τη γρηγορότερη ή την πιο οικονομική διαδρομή. Οι αλγόριθμοι βελτιστοποίησης μπορούν να χρησιμοποιηθούν για να εξασφαλίσουν ότι δεν θα χαθεί πολύτιμος χρόνος ή πόροι κατά τη διάρκεια της αναζήτησης.

Ένας από τους πιο γνωστούς αλγόριθμους βελτιστοποίησης είναι ο **αλγόριθμος Dijkstra**, που χρησιμοποιείται για την εύρεση της συντομότερης διαδρομής ανάμεσα σε δύο σημεία, ιδανικός για προβλήματα όπως η πλοήγηση σε δίκτυα. Αυτός ο αλγόριθμος εξετάζει συστηματικά τις πιθανές διαδρομές και επιλέγει εκείνη που έχει το μικρότερο κόστος.

  1. Πολυπλοκότητα Υπολογισμού

Οι αλγόριθμοι δεν αξιολογούνται μόνο με βάση την αποτελεσματικότητά τους στο να βρίσκουν λύσεις, αλλά και με βάση την υπολογιστική τους πολυπλοκότητα, δηλαδή το πόσο γρήγορα μπορούν να βρουν τη λύση ανάλογα με το μέγεθος του προβλήματος. Ένα μικρό πρόβλημα, όπως ένας μικρός λαβύρινθος, μπορεί να λυθεί γρήγορα με απλό τρόπο. Ωστόσο, καθώς αυξάνεται το μέγεθος του προβλήματος, αυξάνεται και η πολυπλοκότητα.

Η υπολογιστική πολυπλοκότητα μετριέται συχνά σε χρόνο (πόσα βήματα απαιτούνται για την επίλυση) και σε χώρο (πόση μνήμη χρησιμοποιείται). Οι αλγόριθμοι που έχουν σχεδιαστεί για την επίλυση μεγάλων και πολύπλοκων προβλημάτων πρέπει να είναι **αποδοτικοί**, έτσι ώστε να μην καταναλώνουν υπερβολικούς πόρους και να δίνουν λύση σε λογικό χρόνο.

  1. Αλγόριθμοι σε Πραγματικές Εφαρμογές

Οι αλγόριθμοι δεν είναι απλώς αφηρημένες μαθηματικές έννοιες. Εφαρμόζονται σε πραγματικά προβλήματα, από την πλοήγηση GPS μέχρι τη ρομποτική και τα δίκτυα υπολογιστών. Σε ένα σύστημα πλοήγησης, για παράδειγμα, η εύρεση της συντομότερης διαδρομής ανάμεσα σε δύο τοποθεσίες είναι ένα πρόβλημα λαβύρινθου. Οι αλγόριθμοι αναζήτησης χρησιμοποιούνται για να βρουν τη βέλτιστη διαδρομή, ενώ ταυτόχρονα λαμβάνονται υπόψη άλλοι παράγοντες, όπως η κίνηση ή τα εμπόδια.

Στη μηχανική μάθηση, οι αλγόριθμοι αναζητούν πρότυπα και βέλτιστες λύσεις μέσα από τεράστιες ποσότητες δεδομένων, και χρησιμοποιούν τεχνικές που βασίζονται στην ίδια ιδέα της αναζήτησης λύσεων σε πολυπλοκότητα. Ο τρόπος με τον οποίο “εκπαιδεύονται” τα μοντέλα μηχανικής μάθησης για να προβλέψουν ή να αναγνωρίσουν πρότυπα μοιάζει με τη λογική των αλγορίθμων αναζήτησης, καθώς εξετάζονται πολλές επιλογές και διαδρομές.

Συμπέρασμα

Η αναλογία του λαβύρινθου με τα προβλήματα πολυπλοκότητας είναι μια κλασική και αποτελεσματική μεταφορά για να κατανοήσουμε πώς λειτουργούν οι αλγόριθμοι. Μέσα από τον σχεδιασμό και την εφαρμογή αλγορίθμων, είμαστε σε θέση να επιλύουμε περίπλοκα προβλήματα με συστηματικό και αποδοτικό τρόπο. Από τις απλές αναζητήσεις μέχρι τις πιο προχωρημένες μεθόδους βελτιστοποίησης, οι αλγόριθμοι είναι απαραίτητα εργαλεία που μας βοηθούν να βρούμε τη σωστή διαδρομή, ανεξάρτητα από την πολυπλοκότητα του προβλήματος.

Είτε πρόκειται για την εξερεύνηση ενός λαβύρινθου είτε για την πλοήγηση μέσα σε ένα δίκτυο υπολογιστών ή δεδομένων, οι αλγόριθμοι μας προσφέρουν τον καλύτερο τρόπο για να διαχειριστούμε την πολυπλοκότητα και να φτάσουμε στη λύση με το βέλτιστο κόστος και χρόνο.

Η βελτιστοποίηση τοποθέτησης αποτελεί ένα κεντρικό ζήτημα σε πολλούς τομείς της επιστήμης και της τεχνολογίας. Από την οργάνωση αποθηκευτικών χώρων, τη διαχείριση μεταφορών και logistics, μέχρι τον προγραμματισμό και την υπολογιστική γεωμετρία, η αναζήτηση της βέλτιστης τοποθέτησης αντικειμένων σε περιορισμένους χώρους είναι κρίσιμη. Οι αλγόριθμοι είναι τα εργαλεία που μας επιτρέπουν να αντιμετωπίσουμε την πολυπλοκότητα αυτών των προβλημάτων με συστηματικό και αποδοτικό τρόπο, επιδιώκοντας την καλύτερη δυνατή λύση.

Τι είναι η βέλτιστη τοποθέτηση;

Η βέλτιστη τοποθέτηση αναφέρεται στην τοποθέτηση ενός συνόλου αντικειμένων μέσα σε έναν περιορισμένο χώρο με τέτοιο τρόπο ώστε να χρησιμοποιηθεί αυτός ο χώρος όσο το δυνατόν καλύτερα. Στόχος είναι να τοποθετηθούν όσο το δυνατόν περισσότερα αντικείμενα, χωρίς να αφήνονται κενά ή να σπαταλιέται πολύτιμος χώρος. Αυτό το πρόβλημα είναι κλασικό και εντοπίζεται σε εφαρμογές όπως:

– Αποθήκευση προϊόντων: Σε αποθήκες ή βιομηχανικά κέντρα, είναι σημαντικό τα εμπορεύματα να τοποθετούνται με τέτοιο τρόπο ώστε να μεγιστοποιείται η χωρητικότητα της αποθήκης.

– Φόρτωση εμπορευμάτων: Σε μεταφορικά μέσα, όπως φορτηγά, πλοία ή αεροπλάνα, η αποδοτική φόρτωση των προϊόντων μειώνει τον αριθμό των δρομολογίων και κατ’ επέκταση τα κόστη.

– Συσκευασία προϊόντων: Η οργάνωση προϊόντων μέσα σε συσκευασίες, κουτιά ή κοντέινερ πρέπει να βελτιστοποιηθεί, ώστε να χωρέσουν όσο το δυνατόν περισσότερα αντικείμενα.

Η πολυπλοκότητα των προβλημάτων τοποθέτησης

Η πολυπλοκότητα αυτών των προβλημάτων προκύπτει από τον μεγάλο αριθμό παραγόντων και παραμέτρων που πρέπει να ληφθούν υπόψη. Για παράδειγμα, τα αντικείμενα μπορεί να έχουν διαφορετικά μεγέθη και σχήματα, και ο διαθέσιμος χώρος μπορεί να έχει περιορισμούς. Κάθε αντικείμενο πρέπει να τοποθετηθεί με τέτοιο τρόπο ώστε να μην δημιουργούνται κενά και να αξιοποιείται πλήρως ο χώρος.

Σε τέτοια προβλήματα, δεν αρκεί απλά να βρούμε μια λύση· η πρόκληση είναι να βρεθεί η καλύτερη δυνατή λύση, δηλαδή αυτή που μεγιστοποιεί τη χωρητικότητα ή ελαχιστοποιεί το κόστος, ενώ παράλληλα μειώνει τα απόβλητα ή τις σπατάλες πόρων. Αυτή η αναζήτηση της βέλτιστης λύσης απαιτεί τη χρήση αλγορίθμων που μπορούν να χειριστούν πολλαπλές παραμέτρους ταυτόχρονα.

Αλγόριθμοι για τη βέλτιστη τοποθέτηση

Για την αντιμετώπιση της πολυπλοκότητας στη βελτιστοποίηση της χωροθέτησης, χρησιμοποιούνται διάφοροι αλγόριθμοι που αναπτύχθηκαν για να επιλύσουν τέτοιου είδους προβλήματα. Κάθε αλγόριθμος έχει τα δικά του πλεονεκτήματα και μειονεκτήματα, και χρησιμοποιείται ανάλογα με το συγκεκριμένο είδος του προβλήματος και τις απαιτήσεις του.

  1. Αλγόριθμοι Συσκευασίας (Packing Algorithms)

Οι αλγόριθμοι συσκευασίας προσπαθούν να τοποθετήσουν αντικείμενα μέσα σε έναν περιορισμένο χώρο, όπως ένα κουτί, μια αποθήκη ή ένα φορτηγό, με τρόπο που ελαχιστοποιεί τον κενό χώρο και αυξάνει την αποδοτικότητα. Ένα παράδειγμα τέτοιων προβλημάτων είναι το πρόβλημα συσκευασίας κουτιών (**box-packing problem**), στο οποίο πρέπει να τοποθετηθούν αντικείμενα διαφόρων μεγεθών σε κουτιά με συγκεκριμένες διαστάσεις.

Υπάρχουν διάφορες παραλλαγές αυτού του προβλήματος, ανάλογα με το αν τα αντικείμενα μπορούν να τοποθετηθούν κάθετα ή οριζόντια, αν επιτρέπονται επικαλύψεις, ή αν τα κουτιά έχουν σταθερό ή μεταβλητό μέγεθος.

  1. Αλγόριθμος Binning (Bin Packing Algorithm)

Ένας άλλος διαδεδομένος αλγόριθμος είναι ο αλγόριθμος bin packing, ο οποίος χρησιμοποιείται για την τοποθέτηση αντικειμένων σε “δοχεία” (bins). Στόχος είναι να τοποθετηθούν τα αντικείμενα με τέτοιο τρόπο ώστε να χρησιμοποιηθούν όσο το δυνατόν λιγότερα δοχεία, αποφεύγοντας τον άχρηστο χώρο. Αυτός ο αλγόριθμος βρίσκει εφαρμογή στη διαχείριση αποθεμάτων, στις μεταφορές και στη διανομή προϊόντων.

  1. Ευρετικοί αλγόριθμοι

Σε περιπτώσεις όπου τα προβλήματα χωροθέτησης γίνονται εξαιρετικά πολύπλοκα (λόγω του πλήθους των αντικειμένων, των παραμέτρων ή των περιορισμών), οι ευρετικοί αλγόριθμοι χρησιμοποιούνται για να βρουν αποδεκτές λύσεις μέσα σε λογικό χρονικό διάστημα. Οι ευρετικές μέθοδοι δεν εγγυώνται τη βέλτιστη λύση, αλλά παρέχουν μια λύση που είναι κοντά στη βέλτιστη, χωρίς να απαιτούν υπερβολικούς υπολογιστικούς πόρους. Οι αλγόριθμοι γενετικής (genetic algorithms) και οι αλγόριθμοι προσομοιωμένης ανόπτησης (simulated annealing) είναι παραδείγματα ευρετικών μεθόδων που χρησιμοποιούνται σε προβλήματα βελτιστοποίησης.

  1. Αλγόριθμοι Γραμμικού Προγραμματισμού

Για πιο ακριβείς λύσεις, χρησιμοποιούνται συχνά αλγόριθμοι γραμμικού προγραμματισμού. Αυτοί οι αλγόριθμοι επιτρέπουν την επίλυση προβλημάτων βελτιστοποίησης με τη βοήθεια μαθηματικών μοντέλων που χρησιμοποιούν εξισώσεις και ανισώσεις για να καθορίσουν τις καλύτερες δυνατές λύσεις.

Οι αλγόριθμοι γραμμικού προγραμματισμού είναι πολύ αποδοτικοί σε προβλήματα με αυστηρούς περιορισμούς και χρησιμοποιούνται σε εφαρμογές όπως η κατανομή πόρων, η διαχείριση παραγωγής, και οι μεταφορές.

Προκλήσεις και Υπολογιστική Πολυπλοκότητα

Το βασικό πρόβλημα στη βελτιστοποίηση της χωροθέτησης είναι ότι τα προβλήματα αυτά έχουν μεγάλη υπολογιστική πολυπλοκότητα. Καθώς αυξάνεται το πλήθος των αντικειμένων ή των παραμέτρων που πρέπει να εξεταστούν, αυξάνεται και η πολυπλοκότητα του προβλήματος. Η αναζήτηση της βέλτιστης λύσης γίνεται εκθετικά πιο δύσκολη, καθώς κάθε προσθήκη αντικειμένων ή περιορισμών πολλαπλασιάζει τον αριθμό των πιθανών διατάξεων.

Γι’ αυτόν τον λόγο, οι ακριβείς αλγόριθμοι μπορεί να είναι αναποτελεσματικοί σε προβλήματα μεγάλης κλίμακας, και προτιμώνται ευρετικές μέθοδοι που δίνουν γρήγορες και αποδεκτές λύσεις.

Εφαρμογές στην πραγματική ζωή

Τα προβλήματα βελτιστοποίησης της τοποθέτησης και της χωροθέτησης εμφανίζονται σε πολλές εφαρμογές της πραγματικής ζωής:

– Στη βιομηχανία: Οι αλγόριθμοι χωροθέτησης χρησιμοποιούνται για τη βελτιστοποίηση της διάταξης προϊόντων στις αποθήκες, την κατανομή εμπορευμάτων στα μέσα μεταφοράς και την οργάνωση των συστημάτων αποθήκευσης.

– Στις μεταφορές: Οι αλγόριθμοι βελτιστοποίησης εξασφαλίζουν ότι τα οχήματα μεταφοράς χρησιμοποιούνται με τον αποδοτικότερο τρόπο, μειώνοντας τα κόστη και βελτιώνοντας την απόδοση.

– Στην καθημερινή ζωή: Η βελτιστοποίηση της συσκευασίας, όπως η τοποθέτηση αντικειμένων σε μια βαλίτσα, είναι ένα μικρής κλίμακας πρόβλημα χωροθέτησης που όλοι

Συμπέρασμα

Η βελτιστοποίηση της τοποθέτησης είναι ένα πρόβλημα που εμφανίζεται σε πολλές πτυχές της καθημερινής ζωής και της βιομηχανίας. Οι αλγόριθμοι που αναζητούν την καλύτερη δυνατή λύση σε τέτοια προβλήματα αποτελούν κρίσιμο εργαλείο για τη μείωση της σπατάλης χώρου και πόρων, τη βελτίωση της απόδοσης και την εξοικονόμηση κόστους. Καθώς τα προβλήματα αυτά γίνονται πιο πολύπλοκα, οι αλγόριθμοι και οι μέθοδοι βελτιστοποίησης συνεχίζουν να εξελίσσονται, προσφέροντας λύσεις που βοηθούν να επιτευχθεί η μέγιστη αποδοτικότητα σε έναν κόσμο με περιορισμένους πόρους και αυξημένες απαιτήσεις.

«Ψηφιακοί καλλιτέχνες» (20 λεπτά)

Ψηφιακό και αναλογικό – Ψηφιοποίηση και ψηφιακές εικόνες

Η ψηφιοποίηση είναι η διαδικασία μετατροπής της αναλογικής πληροφορίας σε ψηφιακή μορφή, καθιστώντας την κατανοητή και διαχειρίσιμη από υπολογιστικά συστήματα. Με τη μετάβαση από το αναλογικό στο ψηφιακό, η πληροφορία γίνεται πιο ευέλικτη και αποδοτική στη χρήση της, επιτρέποντας την αποθήκευση, την επεξεργασία και τη μετάδοσή της με υψηλή ακρίβεια και μικρότερο κόστος. Αυτό το πέρασμα στην ψηφιακή εποχή είχε τεράστιο αντίκτυπο σε πολλές πτυχές της καθημερινής ζωής, όπως στις επικοινωνίες, την ψυχαγωγία, τις τέχνες, την επιστήμη και τη βιομηχανία.

Αναλογικό και Ψηφιακό: Βασικές Διαφορές

Για να κατανοήσουμε πλήρως την ψηφιοποίηση, πρέπει πρώτα να καταλάβουμε τη διαφορά μεταξύ αναλογικής και ψηφιακής πληροφορίας.

– Αναλογική πληροφορία: Η αναλογική πληροφορία είναι συνεχής και κυμαίνεται με σταθερό τρόπο, αντιπροσωπεύοντας αδιάκοπες μεταβολές στη φυσική κατάσταση της πληροφορίας. Για παράδειγμα, ο ήχος που ακούμε είναι αναλογικός επειδή αποτελείται από κυματομορφές που συνεχώς αλλάζουν την έντασή τους και τη συχνότητά τους. Η αναλογική πληροφορία εκφράζεται σε απεριόριστες τιμές και δεν έχει διακριτές μονάδες. Τα αναλογικά σήματα, όπως αυτά των βινυλίων, των κασετών και των ραδιοφωνικών κυμάτων, αλλάζουν με ροή και συχνά επηρεάζονται από τον θόρυβο και τις αλλοιώσεις λόγω περιβαλλοντικών παραγόντων ή φθοράς.

– Ψηφιακή πληροφορία: Σε αντίθεση, η ψηφιακή πληροφορία είναι διακριτή, δηλαδή αναλύεται σε διακριτές μονάδες, συνήθως με τη μορφή δυαδικών δεδομένων (bits), όπου κάθε τιμή μπορεί να είναι είτε 0 είτε 1. Η ψηφιακή πληροφορία δεν κυμαίνεται συνεχώς, αλλά μετατρέπεται σε έναν ακολουθιακό αριθμό δεδομένων που μπορούν να επεξεργαστούν και να αναπαραχθούν με ακρίβεια από υπολογιστές. Ένα χαρακτηριστικό παράδειγμα είναι οι εικόνες που αποτελούνται από pixels, τα οποία αποθηκεύουν χρώματα και εντάσεις φωτός ως αριθμητικές τιμές.

Η διαδικασία της ψηφιοποίησης

Η ψηφιοποίηση είναι η διαδικασία μετατροπής αναλογικών δεδομένων σε ψηφιακά. Πρόκειται για μια διαδικασία που βασίζεται σε δύο βήματα:

  1. Δειγματοληψία (Sampling): Σε αυτό το στάδιο, το αναλογικό σήμα λαμβάνεται σε διακριτά χρονικά διαστήματα. Αντί να καταγραφεί η συνεχής ροή της πληροφορίας, καταγράφονται συγκεκριμένα σημεία κατά μήκος του σήματος. Όσο περισσότερα δείγματα ληφθούν, τόσο πιο πιστή θα είναι η αναπαράσταση του αρχικού αναλογικού σήματος.
  2. Κβαντοποίηση (Quantization): Αφού ληφθούν τα δείγματα, η τιμή της πληροφορίας κάθε δείγματος μετατρέπεται σε μια αριθμητική τιμή, που αντιπροσωπεύει την πλησιέστερη δυνατή ψηφιακή αντιστοιχία. Οι τιμές αυτές κωδικοποιούνται ως bits. Όσο μεγαλύτερη είναι η ανάλυση της κβαντοποίησης (δηλαδή, όσο περισσότερα bits χρησιμοποιούνται για την κωδικοποίηση), τόσο πιο ακριβής είναι η ψηφιακή αναπαράσταση.

Ψηφιακές Εικόνες και Pixels

Ένα από τα πιο εμφανή παραδείγματα ψηφιοποίησης είναι οι ψηφιακές εικόνες. Όταν μια εικόνα ψηφιοποιείται, διασπάται σε ένα δίκτυο μικροσκοπικών μονάδων που ονομάζονται pixels. Κάθε pixel περιέχει πληροφορίες για το χρώμα και τη φωτεινότητα σε μια συγκεκριμένη θέση στην εικόνα. Έτσι, η αρχική αναλογική εικόνα μετατρέπεται σε ένα σύνολο δεδομένων, τα οποία αποθηκεύονται ψηφιακά και μπορούν να αναπαραχθούν, να επεξεργαστούν ή να μεταδοθούν.

Η ανάλυση μιας ψηφιακής εικόνας εξαρτάται από το πλήθος των pixels. Όσο περισσότερα pixels έχει μια εικόνα, τόσο πιο υψηλής ανάλυσης είναι, κάτι που επιτρέπει την αναπαραγωγή λεπτομερειών. Παράδειγμα είναι μια φωτογραφία υψηλής ανάλυσης, όπου εκατομμύρια pixels συνδυάζονται για να αναπαραστήσουν με ακρίβεια την αρχική εικόνα. Πλεονεκτήματα της Ψηφιοποίησης

Η ψηφιοποίηση προσφέρει πολυάριθμα πλεονεκτήματα σε σύγκριση με τις αναλογικές μορφές πληροφορίας:

  1. Αποθήκευση και ανάκτηση: Τα ψηφιακά δεδομένα μπορούν να αποθηκευτούν με ασφάλεια και να αναπαραχθούν χωρίς απώλειες ποιότητας. Σε αντίθεση με τις αναλογικές μορφές, που μπορεί να φθαρούν με τον καιρό, τα ψηφιακά δεδομένα μπορούν να παραμείνουν αμετάβλητα ανεξάρτητα από το πόσες φορές αναπαράγονται ή αντιγράφονται.
  2. Ακρίβεια και ευκρίνεια: Τα ψηφιακά δεδομένα είναι πολύ πιο ακριβή και μπορούν να αναπαραχθούν χωρίς να επηρεάζονται από θορύβους ή παραμορφώσεις. Για παράδειγμα, μια ψηφιακή εικόνα μπορεί να διατηρήσει την ίδια ποιότητα ανεξάρτητα από το πόσες φορές αποθηκεύεται ή επεξεργάζεται.
  3. Επεξεργασία: Η ψηφιακή πληροφορία είναι πολύ πιο εύκολο να επεξεργαστεί. Εικόνες, ήχοι, βίντεο και κείμενα μπορούν να τροποποιηθούν, να βελτιωθούν ή να αναπαραχθούν μέσω λογισμικών επεξεργασίας, επιτρέποντας τη δημιουργία καινοτόμων έργων και την αποκατάσταση παλαιότερων αρχείων.
  4. Μετάδοση και διανομή: Τα ψηφιακά δεδομένα μπορούν εύκολα να διαμοιραστούν και να μεταδοθούν μέσω του διαδικτύου ή άλλων ψηφιακών δικτύων, επιτρέποντας την ταχύτατη διάδοση πληροφοριών. Για παράδειγμα, ψηφιακά βίντεο μπορούν να μεταδοθούν σε όλο τον κόσμο μέσα σε δευτερόλεπτα, μέσω υπηρεσιών streaming.
  5. Ασφάλεια και προστασία: Η ψηφιακή μορφή επιτρέπει τη χρήση τεχνολογιών κρυπτογράφησης και ασφάλειας για την προστασία των δεδομένων από μη εξουσιοδοτημένη πρόσβαση ή τροποποίηση. Τα ψηφιακά αρχεία μπορούν επίσης να δημιουργήσουν πολλαπλά αντίγραφα ασφαλείας, ώστε να διασφαλιστεί η ακεραιότητα των δεδομένων.

Εφαρμογές της Ψηφιοποίησης

Η ψηφιοποίηση έχει επηρεάσει ποικίλους τομείς της καθημερινής ζωής:

– Ψηφιακή φωτογραφία και τέχνη: Η ψηφιοποίηση των εικόνων επιτρέπει τη διατήρηση και τη δημιουργία ψηφιακών έργων τέχνης, καθώς και τη γρήγορη επεξεργασία και κοινή χρήση φωτογραφιών.

– Ψηφιακή μουσική και ήχος: Οι ήχοι, όπως η μουσική και οι ηχογραφήσεις, μετατρέπονται σε ψηφιακά αρχεία (π.χ. MP3, WAV), διευκολύνοντας την αποθήκευση, την αναπαραγωγή και τη μετάδοσή τους.

– Βίντεο και κινηματογράφος: Οι ταινίες και τα βίντεο που βλέπουμε πλέον έχουν ψηφιοποιηθεί, επιτρέποντας την ταχεία επεξεργασία και τη διάδοσή τους μέσω ψηφιακών πλατφορμών, όπως το YouTube ή τα συστήματα streaming.

– Σαρωτές και αρχεία: Με τη χρήση σαρωτών, τα έγγραφα, τα βιβλία και οι εικόνες μπορούν να ψηφιοποιηθούν, επιτρέποντας την αποθήκευση και τη διάθεσή τους σε ψηφιακές βιβλιοθήκες.

Συμπέρασμα

Η ψηφιοποίηση αποτελεί έναν ακρογωνιαίο λίθο της σύγχρονης τεχνολογίας. Μετατρέποντας την αναλογική πληροφορία σε ψηφιακή, η πληροφορία γίνεται πιο εύκολα διαχειρίσιμη, αποθηκεύσιμη και αναπαραγώγιμη. Αυτή η διαδικασία έχει αλλάξει τον τρόπο που εργαζόμαστε, επικοινωνούμε, δημιουργούμε και αποθηκεύουμε δεδομένα, προσφέροντας αμέτρητες δυνατότητες και βελτιώσεις στην καθημερινή μας ζωή και σε όλους τους κλάδους της τεχνολογίας.

«Στη φαντασία ενός ρομπότ» (20 λεπτά)

Με τον όρο «τεχνητή νοημοσύνη» αναφερόμαστε στον κλάδο της πληροφορικής ο οποίος ασχολείται με τη σχεδίαση και την υλοποίηση υπολογιστικών συστημάτων που μιμούνται στοιχεία της ανθρώπινης συμπεριφοράς τα οποία υπονοούν έστω και στοιχειώδη ευφυΐα, όπως μάθηση, προσαρμοστικότητα, εξαγωγή συμπερασμάτων, κατανόηση από τα συμφραζόμενα, επίλυση προβλημάτων και άλλα.

Η τεχνητή νοημοσύνη αποτελεί σημείο τομής μεταξύ πολλαπλών επιστημών όπως της πληροφορικής, της ψυχολογίας, της φιλοσοφίας, της επιστήμης μηχανικών και άλλων επιστημών με στόχο τη σύνθεση ευφυούς συμπεριφοράς, με στοιχεία συλλογιστικής, μάθησης και προσαρμογής στο περιβάλλον. Η τεχνητή νοημοσύνη εφαρμόζεται τόσο σε μηχανές, όσο και σε υπολογιστές ειδικής κατασκευής και χωρίζεται σε 2 κατηγορίες:

1) Συμβολική τεχνητή νοημοσύνη: η οποία επιχειρεί να εξομοιώσει την ανθρώπινη νοημοσύνη αλγοριθμικά χρησιμοποιώντας σύμβολα και λογικούς κανόνες υψηλού επιπέδου

2) στην υποσυμβολική τεχνητή νοημοσύνη: η οποία αναπαράγει την ανθρώπινη ευφυΐα χρησιμοποιώντας στοιχειώδη αριθμητικά μοντέλα που συνθέτουν επαγωγικά νοήμονες συμπεριφορές κάνοντας χρήση διαδοχικών απλούστερων δομικών συστατικών.

Ανάλογα με τον εκάστοτε επιστημονικό στόχο της, η τεχνητή νοημοσύνη κατηγοριοποιείται και σε άλλου τύπου τομείς όπως επίλυση προβλημάτων, μηχανική μάθηση, ανακάλυψη γνώσης, συστήματα γνώσης και άλλα. Επίσης μπορεί να συνδυαστεί και με άλλους τομείς όπως μηχανική όραση και ρομποτική, τομείς που αποτελούν ανεξάρτητα πεδία εφαρμογής της. Η πιο εντυπωσιακή και γνωστή σε όλο τον κόσμο εφαρμογή της τεχνητής νοημοσύνης είναι το ανθρωποειδές «ρομπότ Σοφία». Κατασκευάστηκε το 2016 από τον καθηγητή Ντέιβιντ Χάνσον (ιδιοκτήτη της εταιρείας Hanson Robotics) και είναι το πρώτο ρομπότ που κατάφερε να μιμηθεί την ανθρώπινη συμπεριφορά, να δείξει τα συναισθήματά του και να συζητήσει με τους ανθρώπους. Μπορεί να μιλήσει πάνω από 20 γλώσσες ανάμεσα σε αυτές και τα Ελληνικά.